挑战GRPO，英伟达提出GDPO，专攻多奖励优化

GRPO 是促使 DeepSeek-R1 成功的基础技术之一。最近一两年，GRPO 及其变体因其高效性和简洁性，已成为业内广泛采用的强化学习算法。

但随着语言模型能力的不断提升，用户对它们的期待也在发生变化：不仅要回答正确，还要在各种不同场景下表现出符合多样化人类偏好的行为。为此，强化学习训练流程开始引入多种奖励信号，每一种奖励对应一种不同的偏好，用来共同引导模型走向理想的行为模式。

但英伟达的一篇新论文却指出，在进行多奖励优化时，GRPO 可能不是最佳选择。

具体来说，在多奖励优化场景中，GRPO 会将不同的奖励组合归一化为相同的优势值。这会削弱训练信号，降低奖励水平。

为了解决这一问题，他们提出了一种新的策略优化方法 —— 组奖励解耦归一化策略优化（GDPO）。该方法通过对各个奖励信号分别进行归一化，避免了不同奖励之间被混合「抹平」，从而更真实地保留它们的相对差异，使多奖励优化更加准确，同时显著提升了训练过程的稳定性。

• 论文标题：GDPO: Group reward-Decoupled Normalization Policy Optimization for Multi-reward RL Optimization

• 论文链接：https://arxiv.org/pdf/2601.05242

• 代码链接：https://github.com/NVlabs/GDPO

• 项目链接：https://nvlabs.github.io/GDPO/

• HuggingFace 链接：https://huggingface.co/papers/2601.05242

  
  

在工具调用、数学推理和代码推理这三类任务上，论文将 GDPO 与 GRPO 进行了对比评测，既考察了正确性指标（如准确率、缺陷比例），也评估了对约束条件的遵守情况（如格式、长度）。结果显示，在所有设置中，GDPO 都稳定地优于 GRPO，验证了其在多奖励强化学习优化中的有效性和良好泛化能力。

GRPO 有什么问题？

目前，GRPO 主要被用于优化单一目标的奖励，通常聚焦于准确率。然而，随着模型能力的持续提升，近期研究越来越倾向于同时优化多个奖励 —— 例如在准确率之外，还考虑响应长度限制和格式质量，以更好地与人类偏好保持一致。现有的多奖励强化学习方法通常采用一种直接的策略：将所有奖励分量相加，然后直接应用 GRPO 进行优化。

具体而言，对于给定的问答对，行为策略会为每个问题采样一组响应。假设存在 n 个优化目标，则第 j 个响应的聚合奖励被计算为各目标奖励之和。随后，通过对群组级别的聚合奖励进行归一化，得到第 j 个响应的群组相对优势。

作者首先重新审视了这种将 GRPO 直接应用于多奖励强化学习优化的常见做法，并发现了一个此前被忽视的问题：GRPO 本质上会压缩奖励信号，导致优势估计中的信息损失。

为了说明这一点，他们从一个简单的训练场景开始，然后推广到更一般的情况。假设为每个问题生成两个 rollout 来计算群组相对优势，且任务涉及两个二值奖励（取值为 0 或 1）。因此，每个 rollout 的总奖励可取 {0, 1, 2} 中的值。

如图 2 所示，作者列举了一个群组内所有可能的 rollout 奖励组合。尽管在忽略顺序的情况下存在六种不同的组合，但在应用群组级奖励归一化后，只会产生两个唯一的优势组。具体来说，(0,1)、(0,2) 和 (1,2) 会产生相同的归一化优势值 (-0.7071, 0.7071)，而 (0,0)、(1,1) 和 (2,2) 则全部归一化为 (0, 0)。

这揭示了 GRPO 优势计算在多奖励优化中的一个根本性局限：它过度压缩了丰富的群组级奖励信号。

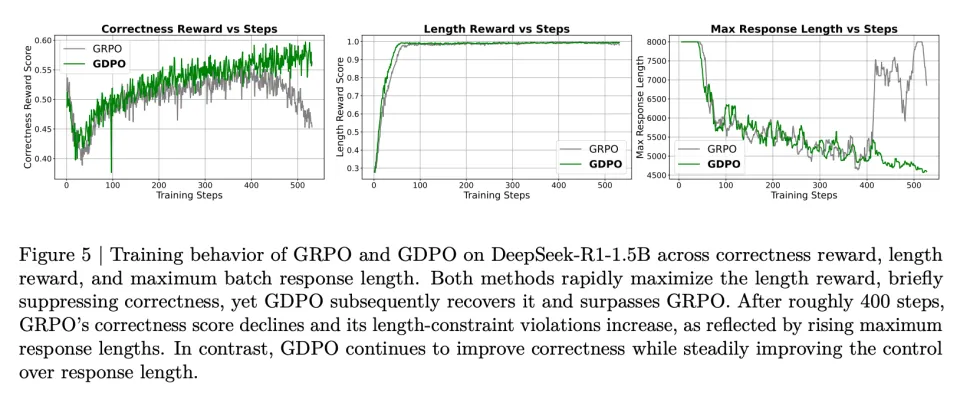
从直觉上讲，(0,2) 应该比 (0,1) 产生更强的学习信号，因为总奖励为 2 意味着同时满足了两个奖励条件，而奖励为 1 仅对应达成一个。因此，当另一个 rollout 只获得零奖励时，(0,2) 应该产生比 (0,1) 更大的相对优势。这种局限性还可能因优势估计不准确而引入训练不稳定的风险。如图 5 所示，当使用 GRPO 训练时，正确率奖励分数在约 400 个训练步后开始下降，表明出现了部分训练坍塌。

近期，Dr.GRPO 和 DeepSeek-v3.2 采用了 GRPO 的一个变体，移除了标准差归一化项，使得优势直接等于原始奖励减去均值。尽管这些工作引入此修改是为了缓解问题级别的难度偏差，但乍看之下，这一改变似乎也能解决上述问题。具体而言，移除标准差归一化确实在一定程度上缓解了问题：(0,1) 和 (0,2) 现在分别产生 (-0.5, 0.5) 和 (-1.0, 1.0) 的不同优势值。

然而，当将此设置推广到更多 rollout（保持奖励数量固定）时，如图 3 所示，作者观察到这种修复方法相比标准 GRPO 仅略微增加了不同优势组的数量。在固定 rollout 数量为 4、逐步增加奖励数量的设置下，也观察到类似趋势 —— 不同优势组的数量仅有适度改善。作者还在第 4.1.1 节中实证检验了移除标准差归一化项的效果，发现这一修改并未带来更好的收敛性或更优的下游评估表现。

GDPO是怎么做的？

为了克服上述挑战，作者提出了群组奖励解耦归一化策略优化（GDPO），这是一种旨在更好地保持不同奖励组合之间区分度、并更准确地在最终优势中捕捉其相对差异的方法。

与 GRPO 直接对聚合奖励和进行群组级归一化不同，GDPO 通过在聚合之前对每个奖励分别进行群组级归一化来解耦这一过程。具体而言，GDPO 不是先将所有 n 个奖励相加再进行群组级归一化得到总优势，而是为第 i 个问题的第 j 个 rollout 的每个奖励分别计算归一化优势，如下所示：

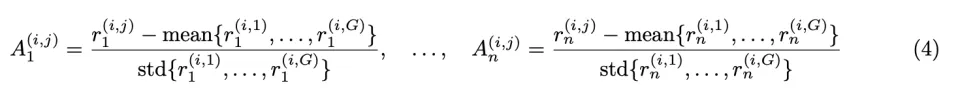
用于策略更新的总体优势通过以下方式获得：首先将所有目标的归一化优势相加，然后对多奖励优势之和应用批次级优势归一化。这确保了最终优势的数值范围保持稳定，不会随着额外奖励的引入而增长。从实证角度，作者还发现这一归一化步骤能够改善训练稳定性。

通过分离每个奖励的归一化，GDPO 缓解了 GRPO 优势估计中存在的信息损失问题，如图 2 所示。从图中可以看到，当采用 GRPO 时，不同的奖励组合（如 (0,2) 和 (0,1)）会导致相同的归一化优势，从而掩盖了它们之间的细微差异。相比之下，GDPO 通过为每种组合分配不同的优势值来保留这些细粒度差异。

作者通过在两种实验设置下比较 GDPO、GRPO 和「无标准差 GRPO」产生的不同优势组数量，进一步量化了 GDPO 的有效性，如图 3 所示。在两个奖励、rollout 数量变化的场景中，GDPO 始终产生显著更多的不同优势组，且随着 rollout 数量增加，差距不断扩大。另一方面，当固定 rollout 数量为 4 并增加奖励数量时，也呈现出类似的模式 ——GDPO 随着目标数量增长表现出逐步增大的优势粒度。这表明论文所提出的解耦归一化方法在所有强化学习设置中都能有效增加不同优势组的数量，从而实现更精确的优势估计。

除了这些理论改进之外，作者还观察到使用 GDPO 能够持续产生更稳定的训练曲线和更好的收敛性。例如，在工具调用任务中，GDPO 在格式奖励和正确率奖励上都实现了更好的收敛，如图 4（见实验部分）所示。GDPO 还消除了 GRPO 在数学推理任务中观察到的训练坍塌问题，如图 5（见实验部分）所示，使用 GDPO 训练的模型在整个训练过程中持续改善正确率奖励分数。实验部分的更多实证结果进一步证实了 GDPO 在广泛的下游任务上实现更强目标偏好对齐的能力。

到目前为止，论文假设所有目标具有同等重要性。然而在实际应用中，这一假设并不总是成立。在论文中，作者系统地概述了如何调整与不同目标相关的奖励权重，或修改奖励函数以强制优先考虑更重要的目标。论文还讨论了当底层奖励在难度上存在显著差异时，这两种设计选择的不同行为表现。具体内容可参见论文第三章。

实验结果如何？

在实验部分，作者首先在工具调用任务上评估 GDPO 与 GRPO 的效果，然后在数学推理任务上进行比较，最后将优化奖励数量扩展到三个，在代码推理任务上进行对比。

工具调用

从图 4 的训练曲线可以看到，GDPO 在所有运行中都能在格式奖励和正确率奖励上收敛到更高的值。尽管 GDPO 在格式奖励收敛所需步数上表现出更大的方差，但最终达到的格式合规性优于 GRPO。对于正确率奖励，GDPO 在早期阶段表现出更快的改善，并在后期达到比 GRPO 基线更高的奖励分数。

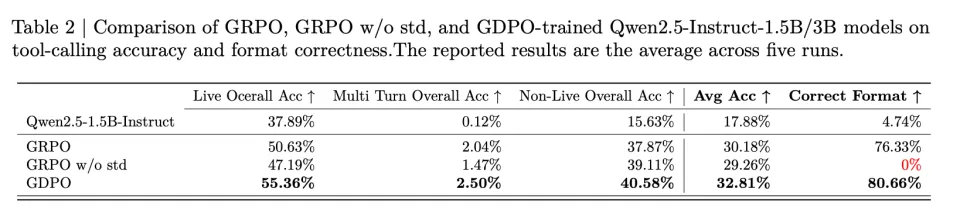
在表 1 的 BFCL-v3 评估中，GDPO 也持续提升了平均工具调用准确率和格式正确率。对于 Qwen2.5-Instruct-1.5B 的训练，GDPO 在 Live/non-Live 任务上分别取得了近 5% 和 3% 的提升，在整体平均准确率上提高了约 2.7%，在正确格式比例上提高了 4% 以上。3B 模型上也观察到类似的改进。

关于移除标准差归一化项的效果：从图 4 可以观察到，虽然「无标准差 GRPO」收敛到与 GDPO 相似且高于标准 GRPO 的正确率奖励，但它在格式奖励上完全失败。这导致在 BFCL-v3 上的正确格式比例为 0%（见表 2），表明模型未能学习所需的输出结构。这说明简单地移除标准差归一化项以增加优势多样性可能会给训练引入不稳定性。

数学推理

从图 5 中 DeepSeek-R1-1.5B 的训练曲线可以看到，模型倾向于最大化更容易的奖励。在本例中，长度奖励更容易优化，GRPO 和 GDPO 都在大约前 100 个训练步内达到满分长度奖励。长度奖励的快速上升伴随着正确率奖励的早期下降，表明这两个奖励存在竞争关系。

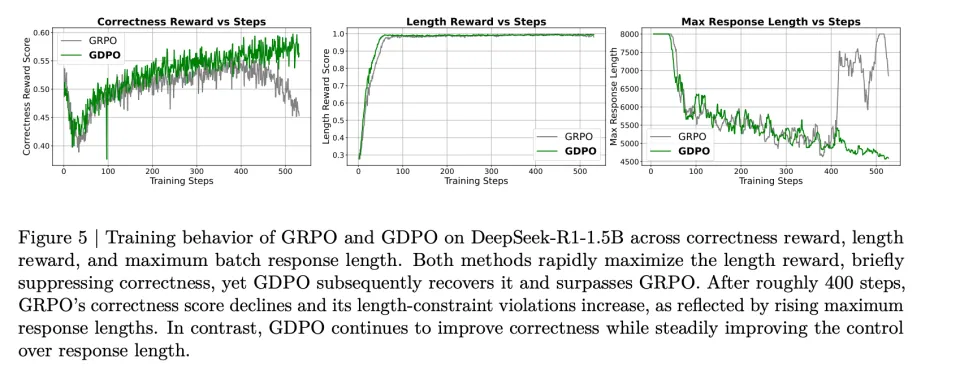
然而，从正确率奖励轨迹来看，GDPO 比 GRPO 更有效地恢复了正确率奖励。作者还观察到 GRPO 训练在 400 步后开始不稳定，正确率奖励分数逐渐下降，而 GDPO 则继续改善。此外，尽管两者都保持了近乎完美的长度分数，但 GRPO 的最大响应长度在约 400 步后开始急剧增加，而 GDPO 的最大响应长度则持续下降。图 9 和图 10 中 DeepSeek-R1-7B 和 Qwen3-4B-Instruct 的训练曲线也显示出类似的观察结果。

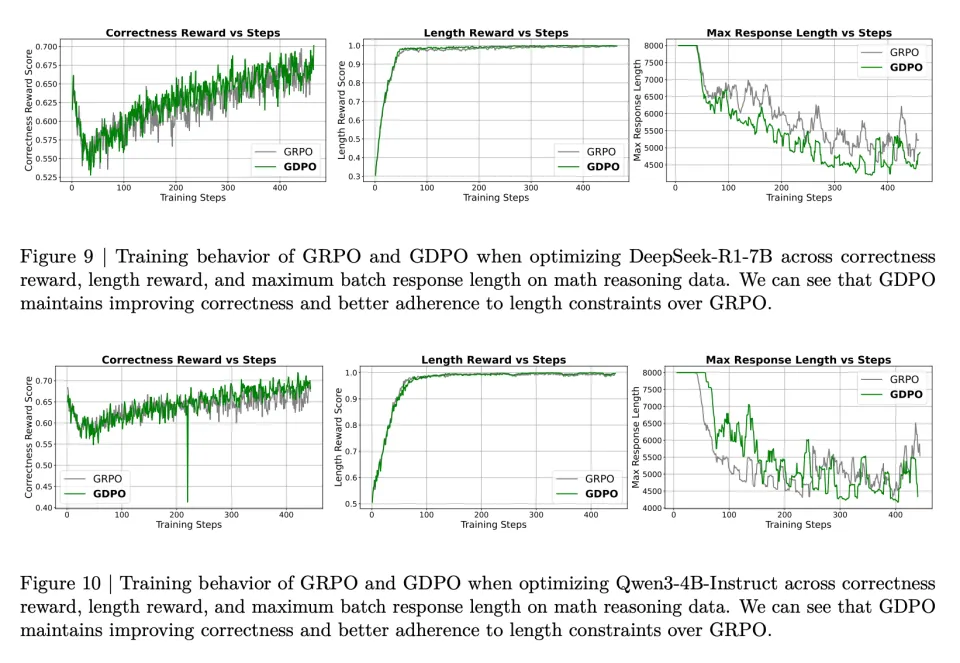
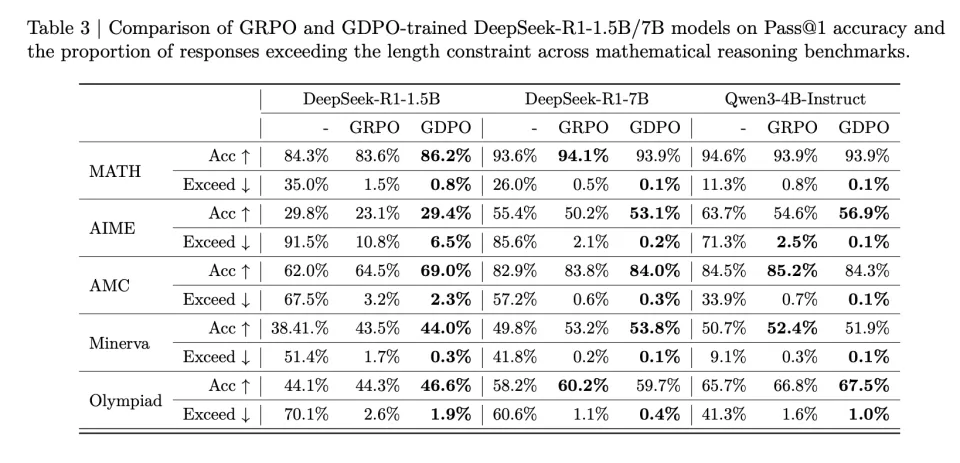
表 3 的基准测试结果表明，GDPO 训练的模型不仅在推理效率上比原始模型取得显著提升（AIME 上超长比例降低高达 80%），而且在大多数任务上也取得了更高的准确率。对于 DeepSeek-R1-1.5B，GDPO 在所有基准测试上都优于 GRPO，在 MATH、AIME 和 Olympiad 上分别取得了 2.6%/6.7%/2.3% 的准确率提升。DeepSeek-R1-7B 和 Qwen3-4B-Instruct 也呈现类似趋势，GDPO 在更具挑战性的 AIME 基准测试上将准确率提高了近 3%，同时将超长率分别降低至 0.2% 和 0.1%。

代码推理

作者在代码推理任务上检验 GDPO 在优化两个以上奖励时是否仍然优于 GRPO。如表 5 所示，在双奖励设置下，GDPO 在所有任务上都提升了通过率，同时保持相似的超长比例。例如，GDPO 在 Codecontests 上将通过率提高了 2.6%，而超长比例仅增加 0.1%；在 Taco 上取得了 3.3% 的通过率提升，同时将超长违规降低了 1%。

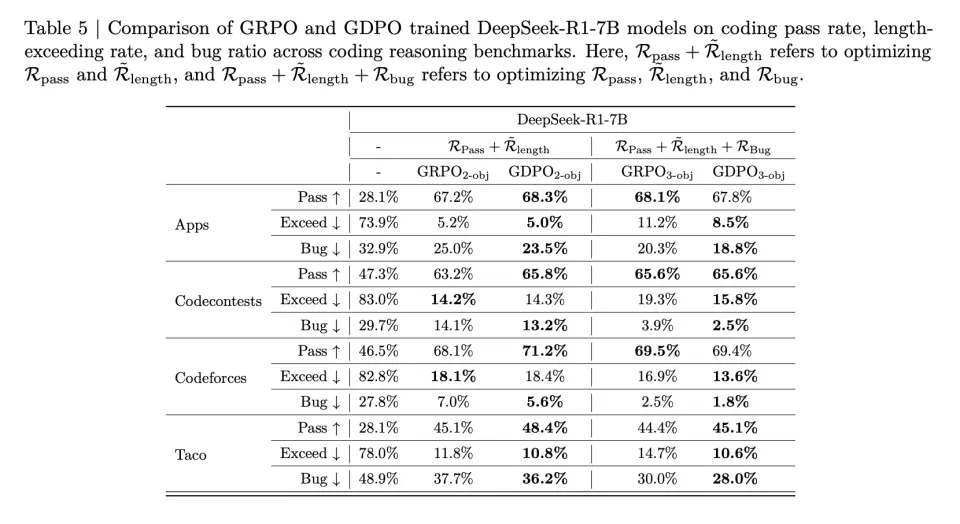
在三种奖励设置下也呈现类似模式，GDPO 在所有目标上都实现了更有利的平衡，在保持与 GRPO 相似通过率的同时，显著降低了超长比例和 bug 比例。

总体而言，这些结果表明 GDPO 在奖励信号数量增加时仍然有效，在双奖励和三奖励配置中都始终比 GRPO 实现更优的跨目标权衡。