大道至简,何恺明团队新作pMF开启像素级「无潜、单步」生成范式
何恺明团队新论文,再次「大道至简」。
此次研究直指当前以 DiT 为代表的主流扩散模型与流匹配模型存在的通病,并提出了一种用于单步、无潜空间(Latent-free)的图像生成新框架。

论文标题:One-step Latent-free Image Generation with Pixel Mean Flows
arXiv 地址:https://arxiv.org/pdf/2601.22158v1
在生成式 AI 领域,追求更高效、更直接的生成范式一直是学界的核心目标。
当前,以 DiT 为代表的主流扩散模型与流匹配模型主要依赖两大支柱来降低生成难度,一是通过多步采样将复杂的分布转换分解为微小的步进,二是在预训练 VAE(变分自编码器)的潜空间中运行以降低计算维度。
尽管这些设计在图像质量上取得了巨大成功,但从深度学习「端到端」的精神来看,这种对多步迭代和预置编码器的依赖,无疑增加了系统的复杂性和推理开销。
面对这些挑战,何恺明团队提出了用于单步、无潜空间图像生成的 pixel MeanFlow(pMF)框架。该框架继承了改进均值流(improved MeanFlow,MF)的思路,通过在瞬时速度(即 v)空间内定义损失函数,来学习平均速度场(即 u)。
与此同时,受 Just image Transformers(JiT)的启发,pMF 直接对类似于去噪图像的物理量(即 x-prediction 值)进行参数化,并预期该物理量位于低维流形上。
为了兼容这两种设计,团队引入了一种转换机制,将 v、u 和 x 三个场联系起来。实验证明,这种设计更符合流形假设,并且产生了一个更易于学习的目标(见下图 1)。
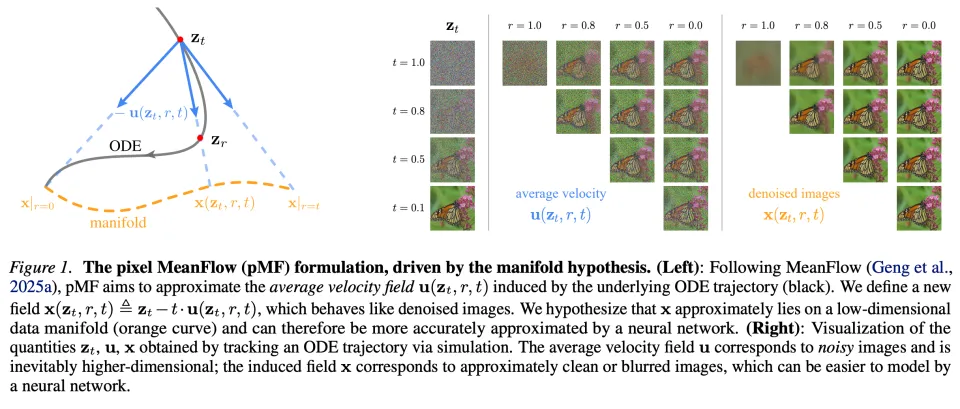
概括来说,pMF 训练了一个能将噪声输入直接映射为图像像素的网络。它具备「所见即所得」的特性,而这在多步采样或基于潜空间的方法中是不存在的。这一特性使得感知损失能够自然地集成到 pMF 中,从而进一步提升生成质量。
实验结果显示,pMF 在单步、无潜空间生成方面表现强劲,在 ImageNet 数据集上,256x256 分辨率下的 FID 达到 2.22,512x512 分辨率下达到 2.48。团队进一步证明,选择合适的预测目标至关重要:在像素空间直接预测速度场会导致性能崩溃。
本文验证了:单步、无潜空间生成正变得既可行又具竞争力,这标志着向构建单一、端到端神经网络形式的直接生成建模迈出了坚实的一步。
框架方法
为了实现单步、无潜空间的生成,团队引入了 pMF(pixel MeanFlow),它的核心设计在于建立 u、 v 和 x 这三个不同场之间的关联。团队希望网络能像 JiT 那样直接输出 x,而单步建模则像均值流 (MeanFlow) 一样在 u 和 v 空间内进行。
去噪图像场
iMF 和 JiT 都可以被视为在最小化 v-loss,不同之处在于 iMF 执行的是 u-prediction,而 JiT 执行的是 x-prediction。团队在 u 与广义形式的 x 之间引入了一种联系。
原论文等式 (5) 中定义的平均速度场 u 代表了一个潜在的基准真值(ground-truth),它取决于 p_data、p_prior 以及时间调度,但与网络无关(因此不依赖于参数 θ)。团队引入了一个定义为 x (z_t, r, t) 的新场:

可泛化的流形假设
上图 1 通过模拟从预训练流匹配(FM)模型中获得的一条 ODE 轨迹,可视化了 u 场和 x 场。u 包含噪声图像,这是因为作为速度场,u 同时包含了噪声和数据成分。相比之下,x 场具有去噪图像的外观:它们或是近乎清晰的图像,或是因过度去噪而显得模糊的图像。接下来,团队讨论了如何将流形假设泛化到一物理量 x 上。
请注意,MeanFlow 中的时间步 r 满足:。团队首先展示了 r=t 和 r=0 这两种边界情况可以近似满足流形假设;随后讨论了 0<r<t 的情况。
算法
上文公式 (8) 中导出的 x 场为 MeanFlow 网络提供了一种重参数化方法。具体而言,团队让网络 net_θ 直接输出 x,并根据公式 (8) 计算出相应的速度场 u:
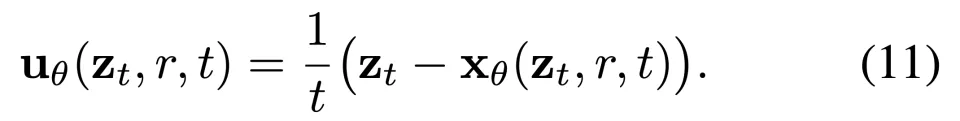
接着将公式 (11) 中的 u_θ 纳入 iMF 表述中,即结合 v-loss 使用原论文公式 (7)。具体的优化目标如下:

从概念上讲,这是基于 x-prediction 的 v-loss,其中 x 通过 x→u→v 的关系转换为 v 空间,从而对 v 进行回归。相应的伪代码见算法 1。遵循 iMF 的思路,该算法可以扩展以支持无分类器引导(CFG)。

带有感知损失的像素均值
网络 x_θ(z_t,r,t) 直接将噪声输入 z_t 映射为去噪图像,这使得模型在训练时具备了「所见即所得」的特性。因此团队进一步引入了感知损失,基于潜空间的方法在 tokenizer 重构训练中获益于感知损失,而基于像素的方法此前尚未能轻易利用这一优势。
在形式上,由于 x_θ 是像素空间下的去噪图像,团队直接对其应用感知损失(例如 LPIPS )。整体训练目标为。在实践中,感知损失可以仅在所添加噪声低于特定阈值(即 t≤t_thr)时应用,从而确保去噪后的图像不会过于模糊。
实验结果
玩具(Toy)实验
团队首先通过一个 2D 玩具实验表明,「当底层数据位于低维流形上时,在 MeanFlow 中使用 x-prediction 更加理想。」
图 2 显示,x-prediction 的表现相当出色,而随着维度 D 的增加,u-prediction 的性能迅速退化。团队观察到,这种性能差距反映在训练损失的差异上:x-prediction 的训练损失低于对应的 u-prediction。这表明,对于容量有限的网络而言,预测 x 更加容易。

团队默认在分辨率为 256x256 的 ImageNet 数据集上进行消融实验。团队采用了 iMF 架构,它是 DiT 设计的一个变体。除非另有说明,团队将 Patch 大小设置为 16× 16(表示为 pMF/16)。消融模型从零开始训练了 160 个 Epoch。
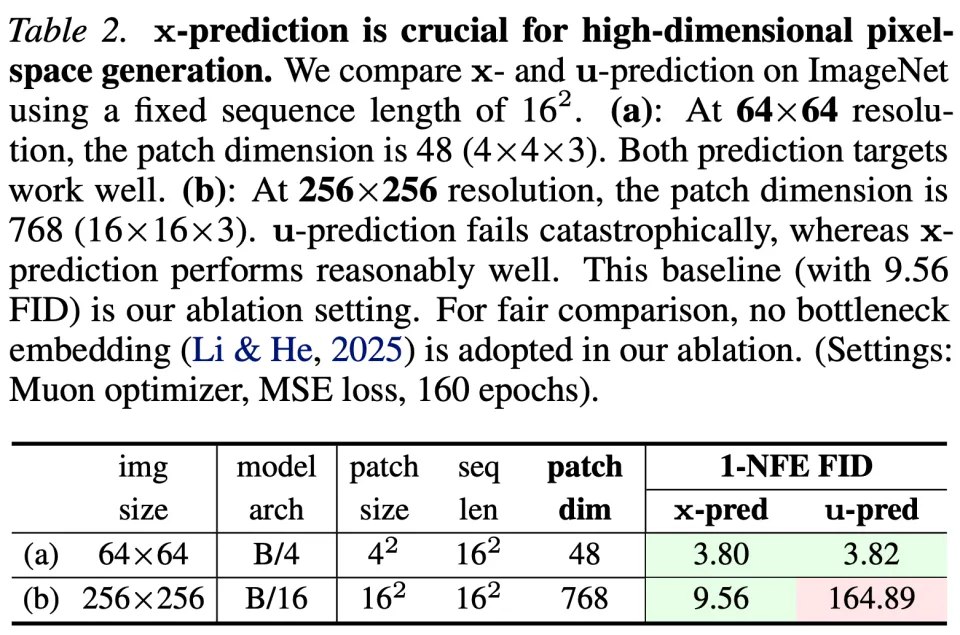
关于网络预测目标,团队的方法基于流形假设,即假设 x 处于低维流形中且更易于预测。表 2 验证了这一假设。
首先将 64×64 分辨率作为较简单的设置。当 Patch 大小为 4×4 时,Patch 维度为 48(即 4×4×3)。这一维度远低于网络容量(隐藏层维度为 768)。因此,pMF 在 x-prediction 和 u-prediction 下均表现良好。
接下来考虑 256×256 分辨率。按照惯例,Patch 大小设为 16×16,Patch 维度达到 768(即 16×16×3)。这导致了更高维的观测空间,增加了神经网络建模的难度。在这种情况下,只有 x-prediction 表现良好,表明 x 位于更低维的流形上,因此更易于学习。
相比之下,u-prediction 性能彻底崩溃:作为一种含噪物理量,u 在高维空间中具有全支撑,建模难度大得多。
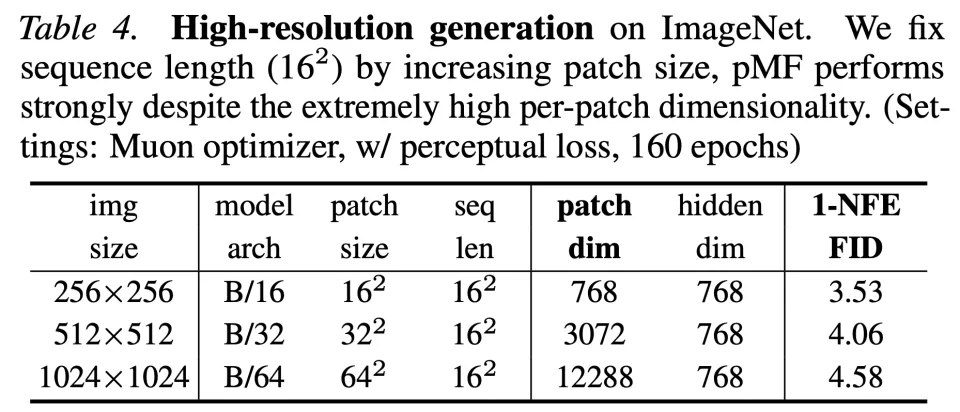
关于高分辨率生成,团队在表 4 中研究了分辨率在 256、512 和 1024 下的 pMF。在保持序列长度不变(16^2)的情况下,不同分辨率下大致维持了相同的计算成本。这样做会导致极其激进的 Patch 大小(例如 64^2)和 Patch 维度(例如 12288)。
结果显示,pMF 可以有效处理这种极具挑战性的情况。尽管观测空间是高维的,但模型始终预测 x,其底层维度并不会成比例增长。
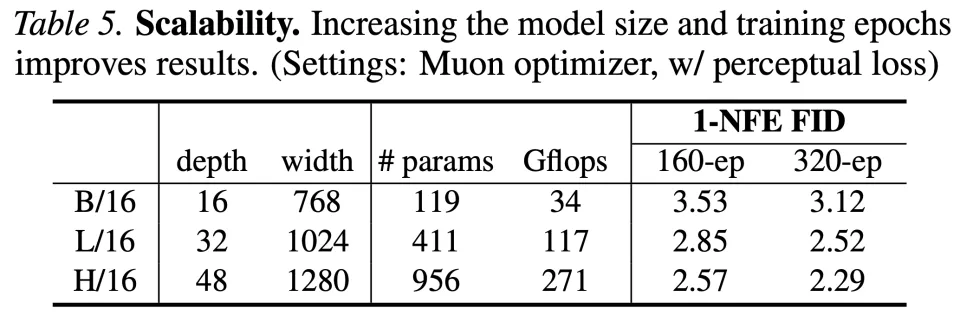
关于可扩展性,团队在表 5 中报告了增加模型大小和训练 Epoch 的结果。正如预期的那样,pMF 从这两个维度的扩展中均有获益。
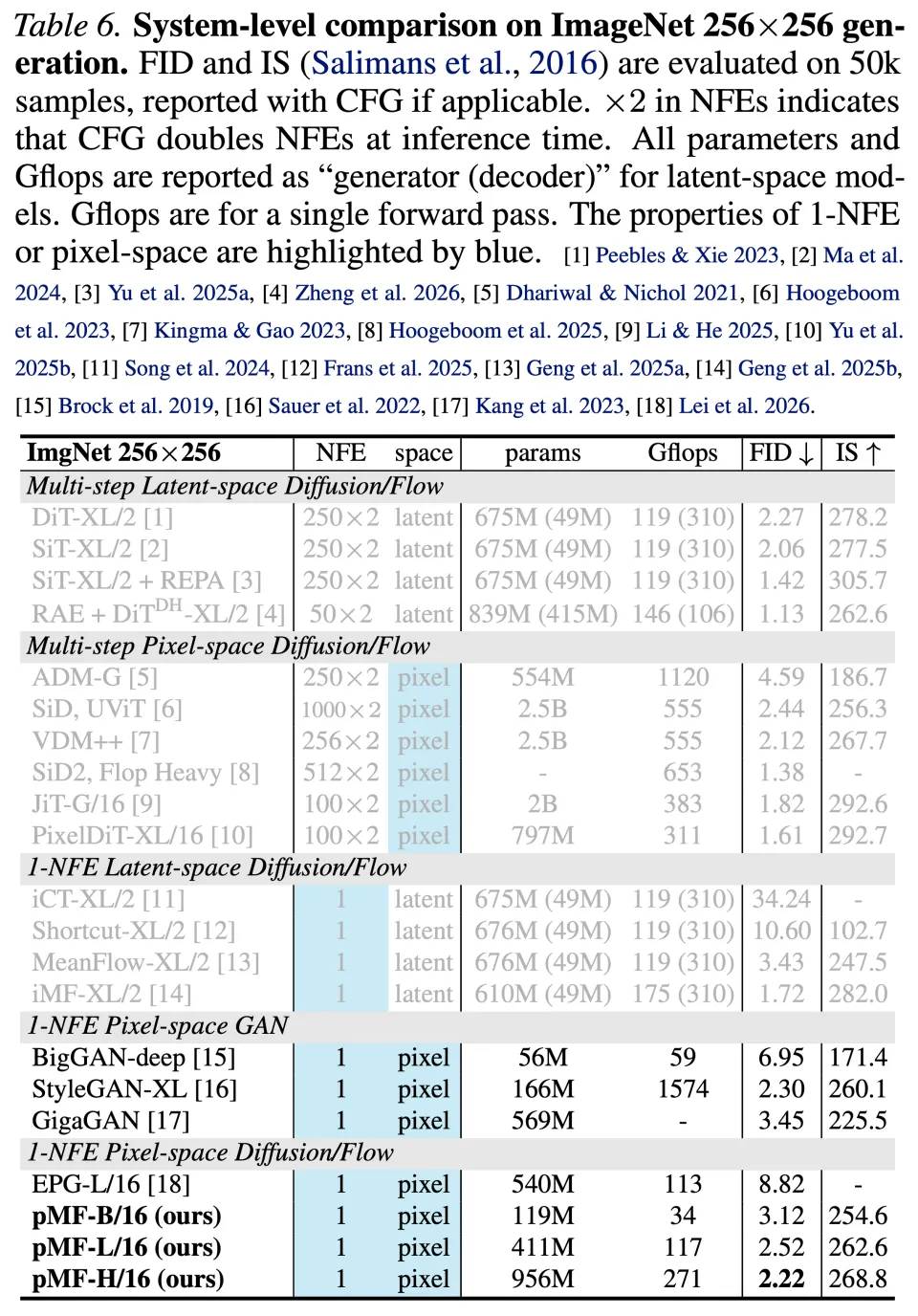
最后,团队在表 6(256×256)和表 7(512×512)中 ,将 pMF 与之前的模型进行了对比。
其中,在 256×256 分辨率下,团队的方法达到了 2.22 FID(在 360 个 Epoch 时),如表 6 所示。据团队的了解,该类别中(单步、无潜空间扩散 / 流模型)唯一的其他方法是最近提出的 EPG,它在自监督预训练下达到了 8.82 FID。
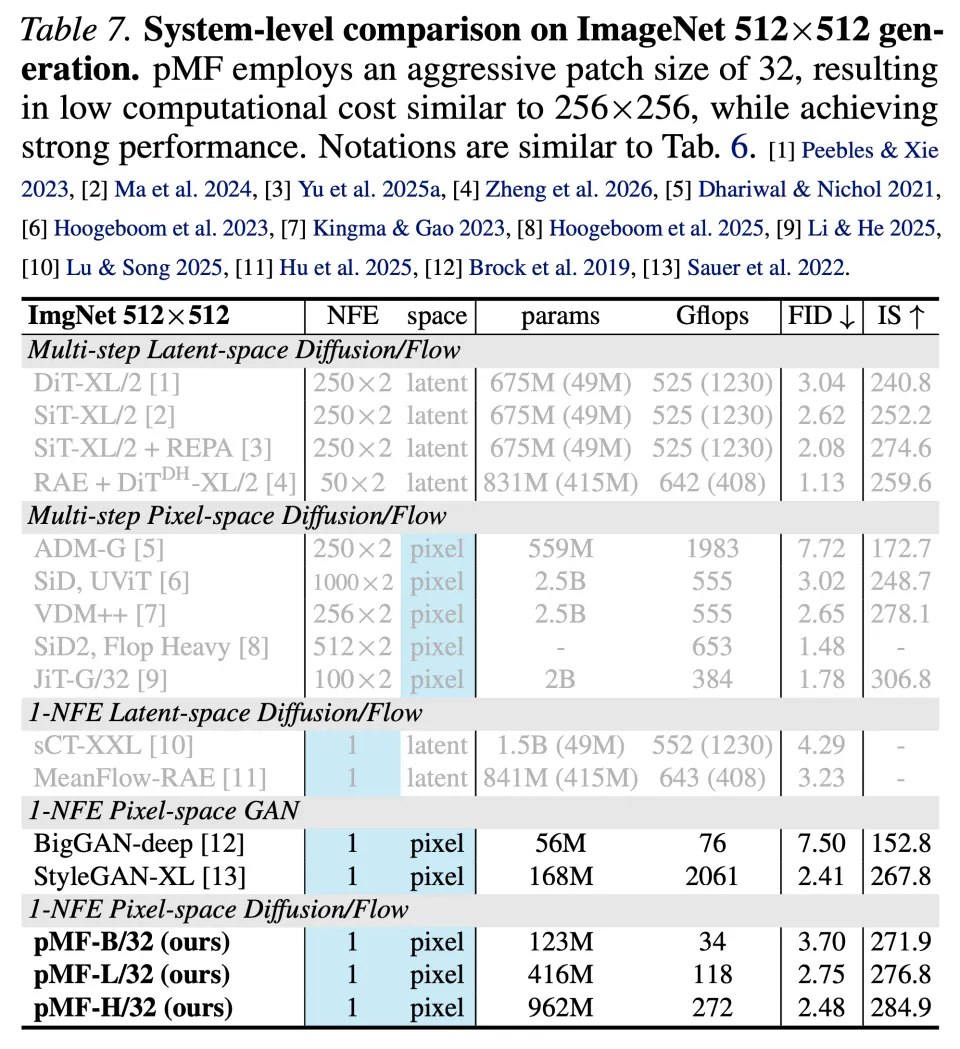
在 512×512 分辨率下,pMF 达到了 2.48 FID,如表 7 所示。这一结果的计算成本(参数量和 Gflops)与 256×256 版本相当。事实上,唯一的额外开销仅来自通道数更多的 Patch 嵌入层和预测层,所有的 Transformer 模块都维持了相同的计算成本。
更多实验细节请参阅原论文。